OBJETIVO
OBJETIVO GENERAL
- Conocer la importancia
del análisis dimensional
OBJETIVO PARTICULAR
- Identificar las variables
y con los grupos adimensionales verificando como influyen estos, en el
desarrollo experimental al obtener datos de flujo volumétrico, área del
orificio, altura con el prototipo para el análisis dimensional.
INTRODUCCIÓN
Es
una técnica mediante la cual se deduce información acerca de un fenómeno,
basándose en la premisa de que este puede escribirse mediante una ecuación
dimensionalmente homogénea entre ciertas variables. El resultado del A.D.
consiste en reducir el número de variables originales que entran en el fenómeno
a un conjunto más pequeño, formado con dichas variables, que conforman un grupo
de parámetros dimensionales.
El análisis dimensional: (1) Permite un
análisis cualitativo. (2) Muestra la dependencia entre las variables. (3)
Simplifica las relaciones entre variables.
Este se basa en el Principio de
Homogeneidad Dimensional, que establece que “si una ecuación expresa
correctamente una relación entre variables, debe ser dimensionalmente
homogénea, es decir, sus sumandos deben tener las mismas dimensiones”.
Una
variable es dimensional si su valor numérico depende de la escala usada
en su medida; esto es, depende del sistema de unidades elegido. Una variable es
adimensional cuando su valor numérico es independiente del sistema de
unidades de medida.
El análisis dimensional permite reducir el
número y la complejidad de las variables que intervienen en la descripción de
un fenómeno físico dado: si un fenómeno físico depende de n variables
dimensionales, es posible reducir el problema a sólo k variables
adimensionales, donde la reducción n-k puede ser 1, 2, 3 o 4,
dependiendo del número de dimensiones básicas que intervengan en el fenómeno.
Aplicaciones en: 1. Detección de errores de cálculo. 2. Resolución de problemas cuya solución
directa conlleva dificultades matemáticas
insalvables. 3. Creación y estudio de modelos reducidos. Por ejemplo, los
túneles aerodinámicos.
DESARROLLO EXPERIMENTAL
RESULTADOS
Tabla 1. Diámetro y área de los
orificios.
N. de orificio
|
Diámetro de orificio(cm)
|
Área cm2
|
1
|
0.238
|
0.044
|
2
|
0.317
|
0.078
|
3
|
0.436
|
0.149
|
4
|
0.555
|
0.241
|
5
|
0.635
|
0.315
|
6
|
1.031
|
0.833
|
7
|
0.423
|
0.140
|
Tabla 2. Altura y flujos volumétricos
N. de orificio
|
Altura (h) cm
|
q=V/t
(ml/s)
|
q=V/t
(ml/s)
|
q=V/t
(ml/s)
|
q=V/t
(ml/s)
|
q=V/t
(ml/s)
|
Promedio
(ml/s)
|
1
|
14
|
7.3442
|
6.2801
|
6.2735
|
6.4070
|
6.3451
|
6.5299
|
2
|
14
|
10.3305
|
11.5646
|
11.0375
|
11.2582
|
11.3122
|
11.1006
|
3
|
14
|
25.1282
|
27.1739
|
26.4864
|
26.3157
|
24.0384
|
25.8285
|
4
|
14
|
37.2549
|
36.4285
|
38.6206
|
41.6
|
37.8571
|
38.3522
|
5
|
14
|
51.2
|
52.0408
|
55.2631
|
55.7692
|
57.8947
|
54.4335
|
6
|
14
|
94.0170
|
82.6666
|
70.3125
|
82.6086
|
64.2173
|
78.7644
|
7
|
14
|
28.7179
|
29.4416
|
28.9915
|
29.7435
|
29.4736
|
29.2736
|
ANÁLISIS DE RESULTADOS
1.
Con los datos obtenidos sustituir en los grupos adimensionales para comprobar
que:
Tabla 3. Calculo de N1
y N2.
No. De orificio
|
N1
|
N2
|
1
|
0.00028428
|
0.00022449
|
2
|
0.00048327
|
0.00039796
|
3
|
0.00112446
|
0.0007602
|
4
|
0.00166969
|
0.00122959
|
5
|
0.0023698
|
0.00160714
|
6
|
0.00342906
|
0.00425
|
7
|
0.00127445
|
0.00071429
|
2.
Calcular el ln de N1 y N2
Tabla 4. Cálculo del Ln
de N1 y N2.
No.
De orificio
|
Ln N1
|
Ln N2
|
1
|
-8.16553792
|
-8.4016803
|
2
|
-7.63493039
|
-7.82916111
|
3
|
-6.79045102
|
-7.18192363
|
4
|
-6.39511766
|
-6.701073
|
5
|
-6.04494978
|
-6.4332973
|
6
|
-5.67546844
|
-5.4608363
|
7
|
-6.66524347
|
-7.24422752
|
3.
Haga una gráfica de lnN1 contra lnN2 y analice la dependencia de las variables
de cada uno.
Grafica 1. Ln de N1
contra Ln de N2.
De la grafica anterior obtenemos la ecuación de
la recta
y = 0.8811x - 0.5679
Donde y es el Ln de N1
y queremos conocer el valor teórico de N1,
sustituyendo a x por el Ln de N2 y
obtenemos los datos de la siguiente tabla.
Tabla 5. Valores de Ln de N2 calculados con la ecuación de
la recta.
No. De orificio
|
N1
|
1
|
0.0003454
|
2
|
0.0005721
|
3
|
0.0010119
|
4
|
0.0015457
|
5
|
0.0019571
|
6
|
0.0046103
|
7
|
0.0009578
|
Como conocemos N1 valor
teórico podemos despejar q(flujo) de N1=
q / g ½ h5/2 y comparar con el resultado experimental.
Despejando tenemos q=N1*
g ½* h5/2
Tabla 6. Cálculo
del flujo teórico
No. De orificio
|
Flujo experimental (cm3/s)
|
Flujo teórico (cm3/s)
|
1
|
6.5299
|
7.9377637
|
2
|
11.1006
|
13.1476393
|
3
|
25.8285
|
23.2548439
|
4
|
38.3522
|
35.5222969
|
5
|
54.4335
|
44.9768308
|
6
|
78.7644
|
105.95099
|
7
|
29.2736
|
22.011552
|
4.
Discuta la magnitud del error (sus posibles causas) y concluya.
Tabla 7. Cálculo del porcentaje de
error.
No. De orificio
|
% de error
|
1
|
17.7
|
2
|
15.5
|
3
|
11.0
|
4
|
7.96
|
5
|
21.0
|
6
|
25.6
|
7
|
32.9
|
El
error pudo deberse a un flujo turbulento dentro del tanque superior o a la
formación de burbujas. También puede que la altura no fuera constante y por
tanto el flujo fuera diferente en cada medida de un mismo agujero. Las
mediciones con cronómetro de mano no suelen ser muy exactas porque está a
merced del rápido reflejo del experimentador (Azzimonti, 2003).
Como
se observa en la tabla 6 el porcentaje de error fue alto esto lo atribuimos a
que la bomba fallaba y se apagaba, esto generaba que la altura variara por 1 o
2 mm y esto afecta ya que la presión con
la que sale el flujo varia.
MEMORIA DE CÁLCULO
·
Tabla
1. Diámetro y área de los orificios.
Se
calculo el area de cada orificio primero se convirtió a cm con la relación
1pulg-------.2.54cm
1/8pulg.------ X
Despejamos
a X que serán los cm equivalentes a 1/8 de pulgada ya que los diámetros de los
orificios estaban en pulgadas para este caso
tenemos:
Observamos
que nos quedan unidades en cm porque las
pulgadas se dividen.
El diámetro se divide entre 2 para obtener el
radio.
·
Tabla
2. Altura y flujos volumétricos
Para esta tabla
calculamos el flujo determinando
experimentalmente en volumen por unidad de tiempo esto es:
Sustituyendo valores
50/4.84
Esto se realizó para
cada orificio para cada una de las tomas y se realizo un promedio.
·
Tabla 3. Cálculo de N1
y N2.
Con las siguientes formulas se calculo N1
y N2.
N1= q / g ½ h5/2
N2= Ao/ h2
Sustituyendo valores en la formulas anteriores
Para N1
Analizando las unidades
Para N2
Analizando las unidades
Tabla 4. Calculo del Ln de N1
y N2.
Se sacó el Ln de N1 y N2.
Tabla 5. Valores de Ln de N2 calculados con la ecuación de
la recta.
y = 0.8811x - 0.5679
donde
y es Ln de N1 y queremos conocer a N1 teórico por lo que se sustituye en X los
valores de N2.
Sustituyendo
valores para el orificio 2:
Tabla 6. Cálculo
del flujo teórico
A continuación se calculo el valor teórico del flujo (q)
para cada orificio con el valor de n1
que se calculo en el punto anterior.
Tenemos
que N1= q / g ½ h5/2
Despejando el flujo:
Sustituyendo valores para el orificio 2:
Analizando las unidades:
Tabla 7. Cálculo del porcentaje de
error.
Se calculó el % de
error con la fórmula
Sustituyendo los
valores de orificio 2:
BIBLIOGRAFÍA
-Azzimonti, J. (2003). Bioestadística aplicada a Bioquímica y Farmacia (2ª ed.). México D. F.: Editorial
Universitaria, pp. 115
-Cengel, Y. y Boles, M. (2006). Termodinámica (6ª ed.). México, D. F.: Editorial McGraw-Hill. ISBN: 970-10-3966-1, pp. 374
-Chang, R. (2010). Química (10ª ed.). E. U. A.:
McGraw-Hill, pp. 256-259









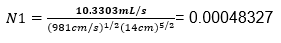






No hay comentarios:
Publicar un comentario
Deja tu comentario, puede ser anónimo. Todos son bienvenidos.