INTRODUCCIÓN
En las
industrias de proceso, la transferencia de calor entre dos fluidos casi siempre
se lleva a cabo en intercambiadores de calor. Entre estos, los de contacto
indirecto son los mas usados pues permiten el manejo higiénico de dos
corrientes independientes, mismas que nunca tienen contacto entre si ya que la
transferencia de calor se realiza a través de una superficie fabricada con
material de alta conductividad térmica. La transferencia de calor se efectúa
por convección desde el fluido caliente a la pared o la superficie de los
tubos, a través de la pared de tubos o placa por conducción, y luego por
convección al fluido frio.
El
equipo de transferencia de calor se define por las funciones que desempeña en
un proceso. Los intercambiadores recuperan calor entre dos corrientes en un
proceso. Los intercambiadores de calor se pueden clasificar en muchas formas
diferentes. Una forma consiste en basar la clasificación en las direcciones
relativas del flujo de los fluidos calientes y frío, dando lugar a términos
como fluidos paralelos, cuando ambos fluidos se mueven en la misma dirección;
flujo encontrado, cuando los fluidos se mueven en paralelo pero en sentido
opuesto; y flujo cruzado, cuando las direcciones de flujo son mutuamente
perpendiculares.
|
|
OBJETIVOS
OBJETIVO
GENERAL
OBJETIVO
PARTICULAR
DESARROLLO
EXPERIMENTAL
Diagrama 1. Determinación del coeficiente global de transferencia en arreglo en paralelo o contracorriente.
Fig. 1 Tipos de arreglos de un intercambiador de calor de
tubos concéntricos.
RESULTADOS
Tabla
A. Datos obtenidos de la tubería para obtener el area de transferencia
Diámetro interno
|
0.015m
|
Diámetro externo
|
0.0327
m
|
Longitud del intercambiador
de calor
|
0.55m
|
Área
|
Tabla
B. Datos obtenidos de la transferencia de calor y la LMTD
Arreglo
|
Qcedido
(kJ/s ó kW)
|
Qganado
(kJ/s ó kW)
|
LMTD (°C)
|
U
|
Paralelo
|
1.20638642
|
1.04110218
|
13.1316
|
|
Contracorriente
|
0.40503088
|
0.40352335
|
12.8562
|
Gráfica 1. Perfil de
temperaturas asociado a un tipo de arreglo en paralelo de un intercambiador de
tubos concéntricos obtenido experimentalmente.
Gráfica 2. Perfil de
temperaturas asociado a un tipo de arreglo en contracorriente de un
intercambiador de tubos concéntricos obtenido experimentalmente.
Gráfica
3. Flujo másico vs calor cedido en flujo en contracorriente.
Gráfica 4. Flujo
másico vs calor cedido en flujo en paralelo.
Gráfica 5. Flujo másico vs U experimental en flujo caliente en paralelo.
Gráfica 6. Flujo másico vs U experimental en flujo frio en paralelo.
Gráfica
7. Flujo másico vs U experimental en flujo caliente en contracorriente.
Gráfica 8. Flujo
másico vs U experimental en flujo frío en contracorriente.
ANÁLISIS
DE RESULTADOS
Los tipos de arreglo de un
intercambiador de tubos concéntricos que se analizarán son paralelo y
contracorriente.
En la
tabla A se muestran las medidas que se tomaron experimentalmente en los tubos,
los cuales se midieron con un vernier y se ocupan para el cálculo del calor
tanto cedido como absorbido, durante el proceso de enfriamiento del agua.
La
tabla B muestra el término diferencia media logarítmica de temperatura se
presenta debido a que la temperatura de uno de los dos fluidos en consideración
varía de acuerdo con su recorrido en la dirección de flujo.
Esta
diferencia debe ser mayor en contracorriente que en paralelo, sin embargo al
comparar la tabla B con la C son muy parecidas esto se debe a que
experimentalmente se tienen errores y pérdidas de temperatura al momento de
tomar la lectura ya que cuando se midió el flujo se esperó a que se llenará la
probeta, lo correcto hubiese sido que se tomará directamente del tubo al
momento de salir el fluido.
Las U
experimentales obtenidas tanto en paralelo como en contracorriente deberían de
ser las mismas o muy parecidas debido a que el calor ganado es igual al calor
cedido, sin embargo se comenten errores
al momento de realizar el experimento como son que pueden existir incrustaciones, suciedad o
fugas en la tubería que estén haciendo que los fluidos entren en contacto y no
se lleve acabo una correcta transferencia de calor. La medición tanto del
volumen, el tiempo y la temperatura son tomadas por diferentes personas, lo
cual hace que el error sea aun mayor.
Al
momento de tomar el volumen con las probetas no se lograba ver bien el volumen
y se tardaba en medirlo y por tanto había un enfriamiento en el agua.
Al
comparar las U experimentales en paralelo las mas cercanas son las del flujo
másico 1 con un error entre ellas de 17%
Y en
el caso del arreglo en contracorriente las más cercanas entre ellas son las del flujo másico 4 que es 0.012 kg/s de
con un error entre ellas de 0.13%
En
general estas U mencionadas anteriormente se pueden considerar como correctas
debido a que cumplen con la ley de la conservación de la materia en donde el calor
cedido igual a calor ganado, y el error que presentan es pequeño comparado con
los demás flujos.
El
perfil de temperaturas asociado con el tipo de arreglo en paralelo cumple con
el comportamiento teórico, en el cual se aprecia que los fluidos entran a una
diferencia de temperaturas considerable y el tiempo que se tardan en lograr un
equilibrio entre ellas es mayor comparado que el perfil de temperaturas de
contracorriente que a pesar de que las temperaturas son diferentes al momento
de entrar a las tuberías la transferencia de calor es mayor y se llega a
temperaturas tanto de enfriamiento como de calentamiento de una manera más
rápida.
Las
graficas de flujo másico contra coeficiente global de transferencia de calor
tanto en paralelo como en contracorriente así como en el fluido caliente como
frio no muestran una tendencia en especifico con la cual se pueda decir que se
tenga un comportamiento especifico sin embargo en la grafica de contracorriente
del fluido caliente se muestra que si aumenta el flujo aumenta el U. De acuerdo
a la fórmula que es Q=U*A*LMTD en donde A es el área y LMTD la diferencia logarítmica
de temperaturas, Q el calor y U el coeficiente de transferencia de calor, se
puede ver que mientras A y LMTD se mantengan constantes el comportamiento
obtenido en la grafica mencionada anteriormente es correcto.
Para
la obtención de los datos teóricos del coeficiente global de transferencia de
calor lo primero que se determinó Reynolds, posteriormente Nusselt y de ahí se
despejo al coeficiente de transferencia de calor tanto en el tubo interno como
en el externo. Obteniendo U como la inversa de la suma de las inversas de los 2
coeficientes.
La
comparación de los U experimentales y de los U teóricos nos dan un error
aproximado muy variados desde el 17% al 96% en donde los errores se le
atribuyen a lo anteriormente mencionado así como a las condiciones ambientales
en las que se lleva acabo el experimento, ya que para el calculo del U teórico
todos los datos se buscan en tablas que ya establecen los valores de los
diámetros de las tuberías así como de las propiedades del fluido utilizado a un
temperatura determinada.
CONCLUSIONES
Los Intercambiadores de Calor permiten el calentamiento o enfriamiento de
un fluido por medio de otro fluido a
diferente temperatura y separado por una pared. En intercambiadores de doble
tubo se puede hacer pasar los fluidos en paralelo o en contracorriente. Si el
arreglo es en paralelo las temperaturas tenderán a igualarse como se observa en
la grafica 1
Si el arreglo es
en contracorriente la temperatura del fluido frio puede calentarse de tal
manera que puede ser en algún punto mayor que la temperatura caliente de
entrada, esto también se observa en la grafica 2.
El coeficiente global de transferencia de calor
de un intercambiador de doble tubo se puede determinar experimentalmente; pero
para obtener resultados confiables deben cuidarse muy bien diversos parámetros
y tener ciertos cuidados en las mediciones.
El error entre los coeficientes globales de
transferencia teoricos y experimentales se debe a errores de medición de los
parámetros que se consideraron.
BIBLIOGRAFÍA
·
Bird,
R., Byron, W.E., Stewart, E.N., Lightfoot. Fenómenos de transporte, un estudio
sistemático de los fundamentos del transporte de materia, energía y cantidad de
movimiento. Reverte, México, 1ª. Edición, 1993.
·
Kern,Donald Q. Procesos de transferencia de
calor. 5° edición. Editorial CECSA. 1999.
MEMORIA
DE CÁLCULO
ARREGLO EN PARALELO
Tabla 1. Datos de temperaturas
obtenidas experimentalmente del arreglo en paralelo a diferentes caudales.
Flujo
|
°T H2O
caliente entrada
(°C)
|
°T H2O
fría entrada (°C)
|
°T H2O
fría salida (°C)
|
°T H2O
caliente salida (°C)
|
||
1
|
35
|
18
|
23
|
25
|
34
|
34
|
2
|
35
|
18
|
20
|
20
|
34
|
34
|
3
|
35
|
18
|
23
|
21
|
33
|
33
|
4
|
35
|
18
|
21
|
22
|
29
|
30
|
5
|
35
|
18
|
24
|
21
|
29
|
29
|
°T=Temperatura
Tabla 2. Datos de el promedio
de las temperaturas de agua fría y deltas de temperaturas de los fluidos
caliente y frio
Flujo
|
Promedio °T H2O
fría salida (°C)
|
Promedio °T H2O caliente salida (°C)
|
**Δ°T del fluido
caliente
|
**Δ°T del fluido
frio
|
1
|
24
|
34
|
1
|
6
|
2
|
20
|
34
|
1
|
2
|
3
|
22
|
33
|
2
|
4
|
4
|
21.5
|
29.5
|
5.5
|
3.5
|
5
|
22.5
|
29
|
6
|
4.5
|
Promedio:22
|
Promedio:31.9
|
|||
** Tomando
en consideración que la temperatura de entrada del agua caliente es de 35°C y
del agua fría 18°C.
Fórmula
utilizada para la obtención de Δ°T
|Promedio °T H2O caliente - °T H2O fría caliente|
= Δ °T (°C ó K)
|Promedio °T H2O fría salida - °T H2O fría
entrada| = Δ °T (°C ó K)
Tabla 3.Datos obtenidos de
volúmenes medidos con la probeta y tiempos tomados con un cronómetro
Flujo
|
Volumen H2O
fría (cm3)
|
Tiempo (s)
|
Volumen H2O
caliente (cm3)
|
Tiempo (s)
|
||||||||
1
|
470
|
450
|
450
|
3.9
|
3.19
|
3.2
|
465
|
462
|
--
|
3.37
|
2.51
|
--
|
2
|
490
|
520
|
470
|
3.3
|
3.6
|
3.36
|
370
|
300
|
--
|
1.68
|
1.08
|
--
|
3
|
520
|
490
|
510
|
3.57
|
3.22
|
3.32
|
425
|
365
|
350
|
2.26
|
1.82
|
2.08
|
4
|
510
|
490
|
490
|
3.68
|
3.51
|
3.5
|
330
|
420
|
355
|
2.24
|
2.09
|
1.71
|
5
|
500
|
520
|
540
|
3.4
|
3.84
|
3.99
|
110
|
150
|
185
|
2.57
|
4.26
|
5.24
|
Tabla 4. Datos del caudal y
flujo másico obtenido en el fluido frio
Flujo
|
Caudales de flujo
frio
(m3/s)
|
Promedio del caudal
(m3/s)
|
Flujo másico (kg/m3)
|
||
1
|
0.00012051
|
0.00014107
|
0.00014063
|
0.00013407
|
0.13406788
|
2
|
0.00014848
|
0.00014444
|
0.00013988
|
0.00014427
|
0.14427008
|
3
|
0.00014566
|
0.00015217
|
0.00015361
|
0.00015048
|
0.15048221
|
4
|
0.00013859
|
0.0001396
|
0.00014
|
0.0001394
|
0.13939603
|
5
|
0.00014706
|
0.00013542
|
0.00013534
|
0.00013927
|
0.13927128
|
Tabla 5. Datos del caudal y
flujo másico obtenido en el fluido caliente
Flujo
|
Caudales de flujo
caliente
(m3/s)
|
Promedio del caudal
(m3/s)
|
Flujo másico (kg/s)
|
||
1
|
0.00013798
|
0.00018406
|
--
|
0.00016102
|
0.16102297
|
2
|
0.00022024
|
0.00027778
|
--
|
0.00024901
|
0.24900794
|
3
|
0.00018805
|
0.00020055
|
0.00016827
|
0.00018562
|
0.18562393
|
4
|
0.00014732
|
0.00020096
|
0.0002076
|
0.00018529
|
0.18529357
|
5
|
4.2802x10-5
|
3.5211x10-5
|
3.5305x10-5
|
3.7773x10-5
|
0.03777272
|
Fórmula
utilizada para la obtención:
Caudal (m3/s) = volumen (m3) /
tiempo (s)
Flujo
másico (kg/s)=caudal (m3/s)=
* densidad (kg/m3)
Tabla 6. Obtención del calor
cedido y absorbido en los diferentes flujos.
Flujo
|
Q absorbido (kJ/s ó kW)
|
Q cedido
(kJ/s ó Kw)
|
Q promedio
(kJ/s ó kW)
|
1
|
3.36322693
|
0.67323704
|
2.01823199
|
2
|
1.20638642
|
1.04110218
|
1.1237443
|
3
|
2.5166645
|
1.55218727
|
2.03442589
|
4
|
2.03985183
|
4.26091825
|
3.15038504
|
5
|
2.62031947
|
0.94756652
|
1.78394299
|
***Tomando
como referencia el Cp a 30°C, el cual es de 4.181 kJ / kg K
Formula utilizada para la obtención del
calor:
m (kg/s)*Cp (kJ /
kg K) * Δ°T (K)=
m(kg/s)*Cp (kJ / kg K) * Δ°T ( K)
Tabla 7. Obtención
del coeficiente global de transferencia.
Flujo
|
LMTD (°C)
|
U fluido frío
(kJ/sm2°C)
|
Ufluido
caliente(kJ/sm2°C)
|
1
|
13.191916
|
0.52479835
|
2.62168572
|
2
|
15.4514926
|
0.69287557
|
0.80287574
|
3
|
13.7830276
|
1.15806204
|
1.87764304
|
4
|
11.9399659
|
3.66971596
|
1.75682245
|
5
|
10.9214477
|
0.8921992
|
2.46721141
|
Cálculo de LMTD
ΔT1= T1-t1
ΔT2=T2-t2
****En donde:
T1=temperatura de entrada del fluido caliente
t1=temperatura de entrada del fluido frio
T2=temperatura de salida del fluido caliente (se consideró la
temperatura promedio de los datos obtenidos experimentalmente)
t2=temperatura de salida de fluido frio (se consideró la temperatura
promedio de los datos obtenidos experimentalmente)
Cálculo
de U teórica
Para obtener ho
Se
obtiene el número de Re para el flujo caliente
Donde
Para obtener el área se considera el
diámetro de la tubería de ½ pulgada obtenida de tablas (Mott,)
Sustituyendo
Así
se calcula el Re para cada flujo por consiguiente se obtienen los siguientes
valores de Re
Tabla
8. Calculo de Re a diferentes flujos másicos
Flujo masico
|
Rec
|
0.16102297
|
17907.78716
|
0.24900794
|
27692.82616
|
0.18562393
|
20643.72402
|
0.18529357
|
20606.98407
|
0.03777272
|
4200.803608
|
Con
la relación que tenemos de Nu propuesta (Kern, 1999) podemos calcular el
coeficiente de película
*Para calcular el numero de Nusselt el
calculo se basa en la correlacion propuesta (Bird, 1993 )
Correlación de Sieder y Tate:
Esta
correlación se utiliza en aplicaciones en donde la influencia de la temperatura
en las propiedades físicas es significativa.
En donde:
μ es la viscosidad evaluada a la temperatura del fluido.
μ0 es la viscosidad evaluada a la temperatura de
la pared.
Consideraciones
de utilización:
§ Esta correlación es válida para los rangos 0,7
< Pr < 16700 y ReD >
104.
§ Las propiedades físicas se deben evaluar a la
temperatura del fluido excepto μ0.
§ Se puede utilizar tanto en cálculos en
condiciones de temperatura de pared y flujo de calor constantes.
Tabla 9. Cálculo de Nu con diferentes Re y el
Pr del agua a temperatura de 32 ºC
Rec
|
Prc
|
Nusselt c
|
17907.78716
|
4.51
|
95.9887249
|
27692.82616
|
4.51
|
136.044349
|
20643.72402
|
4.51
|
107.55166
|
20606.98407
|
4.51
|
107.398504
|
4200.803608
|
4.51
|
30.0921062
|
Obtenido el Nusselt solo se sustituye en
la fórmula.
Donde
Por consiguiente se obtienen los
siguientes datos
Tabla 10. Cálculo de hi con
diferentes Nu
Nusselt c
|
hi
|
95.9887249
|
4501.93572
|
136.044349
|
6380.57141
|
107.55166
|
5044.24516
|
107.398504
|
5037.06202
|
30.0921062
|
1411.34001
|
Para h0 se hace lo anterior
pero con los flujos fríos; pero se considera los diámetros de la tubería
exterior; por tanto el área es:
Y se considera la viscosidad a la
temperatura fría y es 0.001131 kg/ms
Con la anterior consideración se obtienen
los datos de la misma forma que el hi
Tabla 11. Calculo de ho de
diferentes flujos másicos
Flujo masico
|
Ref
|
Nusselt f
|
h0
|
Prf
|
0.13406788
|
22937.0009
|
163.270061
|
10942.7533
|
8.07
|
0.14427008
|
24682.4437
|
173.136157
|
11604.0029
|
8.07
|
0.15048221
|
25745.2458
|
179.074969
|
12002.0363
|
8.07
|
0.13939603
|
23848.567
|
168.440717
|
11289.3031
|
8.07
|
0.13927128
|
23827.2236
|
168.320108
|
11281.2197
|
8.07
|
*El
Pr se usa conforme a la temperatura del fluido frío
Finalmente se obtiene U
Tabla 12. Calculo de U considerando h0
y hi
hi
|
h0
|
U
|
4501.93572
|
10942.7533
|
3189.67717
|
6380.57141
|
11604.0029
|
4116.87081
|
5044.24516
|
12002.0363
|
3551.5789
|
5037.06202
|
11289.3031
|
3483.01165
|
1411.34001
|
11281.2197
|
1254.40707
|
ARREGLO EN CONTRACORRIENTE
Tabla 13. Datos de
temperaturas obtenidas experimentalmente del arreglo en contracorriente a diferentes caudales.
Flujo
|
T° H2O (°C)
caliente entrada
|
T° H2O (°C)
fria entrada
|
T° H2O (°C)
fria salida
|
T° H2O (°C)
caliente salida
|
||||
1
|
35
|
19
|
23
|
22
|
22
|
30
|
34
|
34
|
2
|
35
|
19
|
24
|
21
|
21
|
32
|
33
|
33
|
3
|
35
|
19
|
20
|
20
|
20
|
28
|
32
|
32
|
4
|
35
|
19
|
20
|
20
|
19
|
27
|
27
|
27
|
5
|
35
|
19
|
20
|
20
|
20
|
30
|
30
|
30
|
°T=Temperatura
Tabla 14. Datos del promedio
de las temperaturas de agua fría y deltas de temperaturas de los fluidos
caliente y frio
Flujo
|
Promedio °T H2O
fría salida (°C)
|
Promedio °T H2O
caliente salida (°C)
|
**Δ°T del fluido
caliente
|
**Δ°T del fluido
frio
|
1
|
22.333
|
32.6666667
|
2.33
|
3.33
|
2
|
22
|
32.6666667
|
2.33
|
3
|
3
|
20
|
30.6666667
|
4.33
|
1
|
4
|
19.667
|
27
|
8
|
0.66
|
5
|
20
|
30
|
5
|
1
|
Promedio=20.8
|
Promedio=30.6
|
|||
** Tomando
en consideración que la temperatura de entrada del agua caliente es de 35°C y
del agua fría 19°C.
Fórmula
utilizada para la obtención de Δ°T
|Promedio °T H2O caliente salida - °T H2O fría
entrada| = Δ °T (°C ó K)
|Promedio °T H2O fría salida - °T H2O fría
entrada| = Δ °T (°C ó K)
Tabla 15.Datos obtenidos de
volúmenes medidos con la probeta y tiempos tomados con un cronómetro
Flujo
|
volumen H2O
fria (cm3)
|
tiempo(s)
|
volumen H2O
caliente (cm3)
|
tiempo(s)
|
||||||||
1
|
510
|
560
|
510
|
3.48
|
3.42
|
3.19
|
360
|
310
|
337
|
1.48
|
2.15
|
2.07
|
2
|
510
|
500
|
460
|
3.52
|
3.28
|
3.19
|
330
|
355
|
315
|
2.88
|
3.18
|
3
|
3
|
535
|
530
|
520
|
3.57
|
3.6
|
3.54
|
292
|
345
|
305
|
3.36
|
4.09
|
3.76
|
4
|
510
|
570
|
520
|
3.67
|
3.97
|
3.39
|
150
|
205
|
255
|
12.3
|
17.5
|
20.75
|
5
|
490
|
500
|
420
|
3.64
|
3.39
|
3.1
|
200
|
200
|
210
|
11.1
|
11.2
|
11.62
|
Tabla 16. Datos del caudal y
flujo másico obtenido en el fluido frio
Flujo
|
Caudales de flujo
frio
|
Promedio de
caudales
|
Caudal masico
|
||
1
|
0.00014655
|
0.00016374
|
0.00015987
|
0.00015672
|
0.15672301
|
2
|
0.00014489
|
0.00015244
|
0.0001442
|
0.00014718
|
0.14717534
|
3
|
0.00014986
|
0.00014722
|
0.00014689
|
0.00014799
|
0.14799161
|
4
|
0.00013896
|
0.00014358
|
0.00015339
|
0.00014531
|
0.14531124
|
5
|
0.00013462
|
0.00014749
|
0.00013548
|
0.0001392
|
0.13919729
|
*Los cm3 fueron convertidos a m3
Tabla 17. Datos del caudal y
flujo másico obtenido en el fluido caliente
Flujo
|
Caudales de flujo
caliente
|
Promedio de
caudales
|
Caudal masico
|
||
1
|
0.00024324
|
0.00014419
|
0.0001628
|
0.00018341
|
0.18341041
|
2
|
0.00011458
|
0.00011164
|
0.000105
|
0.00011041
|
0.11040618
|
3
|
8.6905E-05
|
8.4352 x10-5
|
8.1117 x10-5
|
8.4125 x10-5
|
0.08412462
|
4
|
1.2156E-05
|
1.1748 x10-5
|
1.2289 x10-5
|
1.2064 x10-5
|
0.0120642
|
5
|
1.8083E-05
|
1.7921 x10-5
|
1.8072 x10-5
|
1.8026 x10-5
|
0.01802554
|
Fórmula
utilizada para la obtención:
Caudal(m3/s)= volumen (m3) /
tiempo (s)
Flujo
másico (kg/s)=caudal (m3/s)=
* densidad (kg/m3)
Tabla 18. Obtención del calor
cedido y absorbido en los diferentes flujos.
Flujo
|
Qabsorbido
(kJ/s ó kW)
|
Q cedido
(kJ/s ó kW)
|
Q promedio
(kJ/s ó kW)
|
1
|
2.18419631
|
1.7892908
|
1.98674356
|
2
|
1.84602027
|
1.07708593
|
1.4615531
|
3
|
0.61875291
|
1.52414183
|
1.07144737
|
4
|
0.40503088
|
0.40352335
|
0.40427711
|
5
|
0.58198388
|
0.3768239
|
0.47940389
|
***Tomando
como referencia el Cp a 30°C, el cual es de 4.181 kJ / kg K
Formula utilizada para la obtención del
calor:
Q absorbido (kJ/s ó
kW)= Q cedido (kJ/s ó kW)
m (kg/s)*Cp (kJ /
kg K) * Δ°T (K)=
m(kg/s)*Cp (kJ / kg K) * Δ°T ( K)
Cálculo de LMTD
ΔT1= T1-t2
ΔT2=T2-t1
Calculo de U experimental
Para obtener el área se considera el diámetro
equivalente el cual se calculó de la siguiente forma:
Después de haber
obtenido el diámetro equivalente se procedió a calcular el área.
Sustituyendo
Tabla 19. Calculo del LMTD y U fluidos
caliente y frio
LMTD(°C)
|
Ufluido
caliente(kJ/sm2°C)
|
Ufluido frio(kJ/sm2°C)
|
13.16
|
1.3982
|
1.70679
|
13.33
|
0.8309
|
1.42411
|
13.26
|
1.1817
|
0.47975
|
11.27
|
0.3682
|
0.36953
|
12.9
|
0.3005
|
0.46407
|
****En donde:
T1=temperatura de entrada del fluido caliente
t1=temperatura de entrada del fluido frio
T2=temperatura de salida del fluido caliente (se consideró la
temperatura promedio)
t2=temperatura de salida de fluido frio (se consideró la temperatura
promedio)
Calculo
de U teórica
Para obtener ho
Se obtiene el número de Re para el flujo
caliente
Para obtener el área se considera el
diámetro de la tubería de ½ pulgada obtenida de tablas (Mott,)
Así
calculamos el Re para cada flujo por consiguiente se obtienen los siguientes
valores de Re
Tabla
20. Calculo de Re a diferentes flujos masicos
flujo masico
|
Rec
|
0.18341041
|
20397.55278
|
0.11040618
|
12278.56155
|
0.08412462
|
9355.719835
|
0.0120642
|
1341.691316
|
0.01802554
|
2004.667567
|
Con la relación que tenemos de Nu propuesta (Kern, 1999) podemos calcular el
coeficiente de película:
*Para calcular el numero de Nusselt el
calculo se basa en la correlacion propuesta (Bird, 1993)
Correlación de Sieder y Tate:
Esta
correlación se utiliza en aplicaciones en donde la influencia de la temperatura
en las propiedades físicas es significativa.
En donde:
μ es la viscosidad evaluada a la temperatura del fluido.
μ0 es la viscosidad evaluada a la temperatura de
la pared.
Consideraciones
de utilización:
§ Esta correlación es válida para los rangos 0,7
< Pr < 16700 y ReD >
104.
§ Las propiedades físicas se deben evaluar a la
temperatura del fluido excepto μ0.
§ Se puede utilizar tanto en cálculos en
condiciones de temperatura de pared y flujo de calor constantes.
Sustitución en la ecuación considerando
el número de Pr obtenido de tablas para la temperatura en la cual se maneja el
fluido y se obtienen los siguientes valores
Tabla 21. Calculo
de Nu con diferentes Re y el Pr del agua a temperatura de 32 ºC
Rec
|
Prc
|
Nusselt c
|
20397.55278
|
4.51
|
106.52441
|
12278.56155
|
4.51
|
70.9748816
|
9355.719835
|
4.51
|
57.1016227
|
1341.691316
|
4.51
|
12.0756014
|
2004.667567
|
4.51
|
16.6502429
|
Obtenido el Nusselt sólo se sustituye en
la fórmula
Por consiguiente se obtienen los
siguientes datos
Tabla 22. Cálculo de hi con
diferentes Nu.
Nusselt c
|
hi
|
106.52441
|
4996.06641
|
70.9748816
|
3328.76965
|
57.1016227
|
2678.10448
|
12.0756014
|
566.353824
|
16.6502429
|
780.907585
|
Para h0 se hace lo anterior
pero con los flujos frios; pero se considera los diámetros de la tubería
exterior; por tanto el área es:
Y se considera la viscosidad a la
temperatura fria y es 0.001131 kg/ms
Con la anterior consideración se obtienen
los datos de la misma forma que el hi
Tabla 23. Cálculo de ho de
diferentes flujos másicos.
flujo masico
|
Ref
|
Nussetl f
|
h0
|
Prf
|
0.15672301
|
26812.9522
|
184.992004
|
12398.6103
|
8.07
|
0.14717534
|
25179.4895
|
175.919826
|
11790.571
|
8.07
|
0.14799161
|
25319.1408
|
176.699948
|
11842.8567
|
8.07
|
0.14531124
|
24860.5711
|
174.135024
|
11670.9493
|
8.07
|
0.13919729
|
23814.5659
|
168.248571
|
11276.4251
|
8.07
|
*El
Pr se usa conforme a la temperatura del fluido frío
Finalmente se obtiene U
Sustituyendo se obtiene
Tabla 24. Cálculo de U considerando h0
y hi
hi
|
h0
|
U
|
4996.06641
|
12398.6103
|
3561.10559
|
3328.76965
|
11790.571
|
2595.88668
|
2678.10448
|
11842.8567
|
2184.18101
|
566.353824
|
11670.9493
|
540.14244
|
780.907585
|
11276.4251
|
730.33117
|

















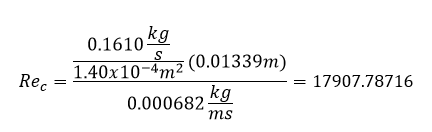
















No hay comentarios:
Publicar un comentario
Deja tu comentario, puede ser anónimo. Todos son bienvenidos.