OBJETIVOS
1.
Determinar
la constante cinética de pseudoprimer orden, k1, de la decoloración
de la fenolftaleína en disolución alcalina.
2.
Determinar
la constante cinética de segundo orden, k, de la decoloración de la
fenolftaleína.
3.
Determinar
el efecto de la concentración de hidróxido en la cinética de decoloración de la
fenolftaleína.
4.
Determinar
el efecto de la fuerza iónica en la decoloración de la fenolftaleína.
INTRODUCCIÓN
La fenolftaleína se usa como ingrediente activo en algunos laxantes pero más familiarmente como un indicador ácido-base para detectar el punto de equivalencia en las titulaciones. Si se encuentra un exceso de base en el matraz al final de la titulación, el estudiante notará que el color rosa de la fenolftaleína desaparece después de un rato. Esta decoloración no es consecuencia de la titulación y sin pensarlo más, la disolución se desecha. Sin embargo el por qué sucede esta decoloración es interesante y en esta práctica se abordará el problema desde el punto de vista cinético.
A pesar de que la fenolftaleína es uno de los indicadores más utilizados, su química no es simplemente la de un par conjugado ácido-base, HIn-In-. Las formas en que se encuentra la fenolftaleína en disolución (alcohólica-acuosa) se presentan en el esquema 1. La fenolftaleína es incolora a pH ≤ 8. La forma incolora tiene la estructura 1 y la abreviamos como H2F. A medida que el pH se incrementa de 8 a 10, los protones fenólicos son neutralizados con aproximadamente la misma facilidad y el anillo de la lactona se abre produciendo el familiar color rosado correspondiente a la estructura 2, abreviada como F2-. A pHs mayores, el color rosa desaparece lentamente debido a la existencia de la estructura 3, abreviada como FOH3-. Todos los cambios de color son reversibles. La conversión de H2F a F2- es extremadamente rápida y esencialmente completa al momento de alcanzarse un pH = 11, mientras que la conversión de F2- a FOH3- a pHs mayores de 11 es suficientemente lenta para que su velocidad pueda ser medida espectrofotométricamente.
La decoloración de la fenolftaleína en medio básico, se puede representar con la siguiente ecuación:
la ley de velocidad puede expresarse como:
El procedimiento experimental implica la utilización de disoluciones fuertemente básicas que contienen solo trazas de fenolftaleína, de tal manera que la concentración de OH- excede la de la fenolftaleína por un factor de por lo menos 104 veces. Por lo tanto, durante cada corrida, la concentración de OH- permanece prácticamente constante y la ley de velocidad se simplifica a :
en esta nueva ley de velocidad,
METODOLOGÍA
Determinación de la constante cinética de pseudoenésimo orden para la decoloración de la fenolftaleína en medio básico.
- Preparar 10 ml de las disoluciones de NaOH que se indican en la tabla 1, primero para una corrida y luego para la otra.
- Ajustar el espectrofotómetro a cero de absorbancia a 550 nm con el blanco.
- Añadir una gota de fenolftaleína a los tubos 1 y 2. Homogeneizar y comenzar a contar el tiempo. Tomar lecturas de absorbancia cada 2 minutos durante 20 min.
- Añadir una gota de fenolftaleína al tubo 3. Homogeneizar y comenzar a contar el tiempo. Tomar lecturas de absorbancia cada minuto hasta la desaparición del color rosa.
- Colocar la disolución del tubo 4 en una cubeta para el espectrofotómetro, añadir una gota de disolución de fenolftaleína e invertir varias veces la cubeta para homogeneizar. Contar el tiempo a partir de la adición de la fenolftaleína. Tomar las lecturas de absorbancia a 550 nm cada 30 seg hasta la desaparición del color rosa.
- Colocar la disolución del tubo 5 en una cubeta para el espectrofotómetro, añadir una gota de disolución de fenolftaleína e invertir varias veces la cubeta para homogeneizar. Contar el tiempo a partir de la adición de la fenolftaleína. Tomar las lecturas de absorbancia a 550 nm cada 30 seg hasta la desaparición del color rosa.
- Repetir el procedimiento para una segunda corrida.
Determinación del efecto de la fuerza iónica en la velocidad de decoloración de la fenolftaleína.
- Preparar 10 ml de las disoluciones a la fuerza iónica que se indica en la tabla 2, primero para una corrida y luego para la otra.
- Ajustar el espectrofotómetro a cero de absorbancia a 550 nm con el blanco.
- Añadir una gota de fenolftaleína a los tubos 6 y 7. Homogeneizar y comenzar a contar el tiempo. Tomar lecturas de absorbancia cada 2 minutos durante 20 min.
- Añadir una gota de fenolftaleína al tubo 8. Homogeneizar y comenzar a contar el tiempo. Tomar lecturas de absorbancia cada minuto hasta la desaparición del color rosa.
- Colocar la disolución del tubo 9 en una cubeta para el espectrofotómetro, añadir una gota de disolución de fenolftaleína e invertir varias veces la cubeta para homogeneizar. Contar el tiempo a partir de la adición de la fenolftaleína. Tomar las lecturas de absorbancia a 550 nm cada 30 seg hasta la desaparición del color rosa.
- Colocar la disolución del tubo 10 en una cubeta para el espectrofotómetro, añadir una gota de disolución de fenolftaleína e invertir varias veces la cubeta para homogeneizar. Contar el tiempo a partir de la adición de la fenolftaleína. Tomar las lecturas de absorbancia a 550 nm cada 30 seg hasta la desaparición del color rosa.
- Repetir el procedimiento para una segunda corrida.
RESULTADOS
Experimento b1
Tabla 1. Características de las soluciones preparadas en los tubos. La fuerza
iónica se mantuvo constante mientras se varió la concentración de OH-. En la
tabla se muestra la concentración de OH- esperada y la concentración de OH- que
realmente se agregó a los tubos.
Tubo
|
[OH-]
(M)
|
[OH-]
real (M)
|
Volumen
de NaOH 0.3 M
(ml)
|
Volumen
de NaCl 0.3 M
(ml)
|
Fuerza
iónica
(M)
|
1
|
0.025
|
0.024
|
0.8
|
9.2
|
0.3
|
2
|
0.05
|
0.051
|
1.7
|
8.3
|
0.3
|
3
|
0.1
|
0.099
|
3.3
|
6.7
|
0.3
|
4
|
0.2
|
0.201
|
6.7
|
3.3
|
0.3
|
5
|
0.3
|
0.3
|
10
|
0
|
0.3
|
Tabla 2. Resultados del experimento b1 para el
efecto de la concentración de OH- en la velocidad de decoloración de
fenolftaleína (absorbancias a 550 nm).
TUBO
1
|
TUBO
2
|
TUBO
3
|
TUBO
4
|
TUBO
5
|
|||||
Tiempo
(min)
|
ABS
|
Tiempo
|
ABS
|
Tiempo (min)
|
ABS
|
Tiempo (min)
|
ABS
|
Tiempo (min)
|
ABS
|
0
|
1.475
|
0
|
1.199
|
0
|
1.022
|
0
|
0.909
|
0
|
1.114
|
2
|
1.425
|
2
|
1.107
|
1
|
0.947
|
0.5
|
0.833
|
0.5
|
0.981
|
4
|
1.382
|
4
|
1.025
|
2
|
0.879
|
1
|
0.766
|
1
|
0.864
|
6
|
1.341
|
6
|
0.95
|
3
|
0.816
|
1.5
|
0.703
|
1.5
|
0.763
|
8
|
1.303
|
8
|
0.883
|
4
|
0.759
|
2
|
0.647
|
2
|
0.671
|
10
|
1.27
|
10
|
0.822
|
5
|
0.705
|
2.5
|
0.595
|
2.5
|
0.592
|
12
|
1.236
|
12
|
0.767
|
6
|
0.657
|
3
|
0.548
|
3
|
0.523
|
14
|
1.204
|
14
|
0.716
|
7
|
0.611
|
3.5
|
0.505
|
3.5
|
0.462
|
16
|
1.174
|
16
|
0.67
|
8
|
0.57
|
4
|
0.466
|
4
|
0.409
|
18
|
1.144
|
18
|
0.628
|
9
|
0.531
|
4.5
|
0.43
|
4.5
|
0.363
|
20
|
1.116
|
20
|
0.59
|
10
|
0.496
|
5
|
0.397
|
5
|
0.321
|
11
|
0.463
|
5.5
|
0.367
|
5.5
|
0.285
|
||||
12
|
0.433
|
6
|
0.339
|
6
|
0.254
|
||||
13
|
0.405
|
6.5
|
0.314
|
6.5
|
0.226
|
||||
14
|
0.38
|
7
|
0.291
|
7
|
0.202
|
||||
15
|
0.356
|
7.5
|
0.27
|
7.5
|
0.18
|
||||
16
|
0.335
|
8
|
0.25
|
8
|
0.162
|
||||
17
|
0.315
|
8.5
|
0.232
|
8.5
|
0.145
|
||||
18
|
0.297
|
9
|
0.216
|
9
|
0.13
|
||||
19
|
0.279
|
9.5
|
0.201
|
9.5
|
0.118
|
||||
20
|
0.264
|
10
|
0.187
|
10
|
0.106
|
||||
21
|
0.249
|
10.5
|
0.174
|
10.5
|
0.097
|
||||
22
|
0.235
|
11
|
0.163
|
11
|
0.089
|
||||
23
|
0.222
|
11.5
|
0.152
|
11.5
|
0.081
|
||||
24
|
0.211
|
12
|
0.142
|
12
|
0.075
|
||||
25
|
0.2
|
12.5
|
0.133
|
||||||
26
|
0.19
|
13
|
0.125
|
||||||
27
|
0.181
|
13.5
|
0.118
|
||||||
14
|
0.111
|
||||||||
14.5
|
0.105
|
||||||||
15
|
0.099
|
||||||||
15.5
|
0.093
|
||||||||
16
|
0.088
|
Figura 1.
Gráfico de la absorbancia contra el tiempo para la determinación de una
cinética de orden cero.
Figura
2. Gráfica del logaritmo natural de la absorbancia contra el tiempo para
la determinación de una cinética de primer orden.
Tabla 6.
Resultados del experimento b2 para la determinación del efecto de la fuerza
iónica en la velocidad de decoloración de fenolftaleína.
DISCUSIÓN
CONCLUSIONES
BIBLIOGRAFÍA
ANEXOS
Memoria de cálculos
Integración de velocidades para orden cero, uno y dos
Tablas
Figura 3. Gráfica del inverso de la absorbancia contra el tiempo para la determinación
de una cinética de segundo orden.
Tabla 3. Valores de las constantes de regresión para los tubos 1-5 del
experimento b1.
ORDEN CERO
|
|||
m
|
b
|
r2
|
|
Tubo
1
|
-0.0177
|
1.4556
|
0.9928
|
Tubo
2
|
-0.03
|
1.1511
|
0.982
|
Tubo
3
|
-0.0291
|
0.8571
|
0.924
|
Tubo
4
|
-0.0459
|
0.6995
|
0.883
|
Tubo
5
|
-0.0765
|
0.8275
|
0.8586
|
ORDEN
UNO
|
|||
m
|
b
|
r2
|
|
Tubo
1
|
-0.0138
|
0.3801
|
0.9979
|
Tubo
2
|
-0.0354
|
0.1674
|
0.9987
|
Tubo
3
|
-0.0644
|
-0.0325
|
0.9969
|
Tubo
4
|
-0.1468
|
-0.1682
|
0.9968
|
Tubo
5
|
-0.2281
|
0.0418
|
0.9974
|
ORDEN DOS
|
|||
m
|
b
|
r2
|
|
Tubo
1
|
0.0108
|
0.6798
|
0.9998
|
Tubo
2
|
0.043
|
0.8054
|
0.9961
|
Tubo
3
|
0.1675
|
0.5431
|
0.9726
|
Tubo
4
|
0.6254
|
-0.1981
|
0.9466
|
Tubo
5
|
1.0044
|
-0.8975
|
0.9235
|
Tabla 4. Datos para la determinación de la constante, k, de reacción. Los
datos están tomados de las tablas 1 y 3.
OH-
(M)
|
k1
|
ln
(OH-)
|
ln
k1
|
0.024
|
0.0138
|
-3.72970145
|
-4.28308669
|
0.051
|
0.0354
|
-2.97592965
|
-3.34104346
|
0.099
|
0.0644
|
-2.31263543
|
-2.74264165
|
0.201
|
0.1468
|
-1.60445037
|
-1.91868416
|
0.3
|
0.2281
|
-1.2039728
|
-1.47797115
|
Figura
4. Determinación de la constante, k, global de reacción donde k1=kCmOH-
y lnk1=mlnCOH- + ln k. Se obtiene un valor de m de 1 y un
valor de k de 0.851036.
Experimento b2
Tabla 5. Datos de las soluciones preparadas para el experimento b2 donde la
concentración de NaOH se mantuvo
constante a 0.021 M mientras se varió la fuerza iónica de las soluciones. Se
muestra la fuerza iónica que se trató y la fuerza iónica real que se logró debido
a la precisión de los instrumentos.
Tubo
|
Fuerza
iónica deseada
(M)
|
Fuerza
iónica real
(M)
|
Volumen
de NaOH 0.3 M
(ml)
|
Volumen
de NaCl 0.3 M
(ml)
|
Volumen
de agua (ml)
|
6
|
0.025
|
0.027
|
0.7
|
0.2
|
9.1
|
7
|
0.05
|
0.051
|
0.7
|
1
|
8.3
|
8
|
0.1
|
0.102
|
0.7
|
2.7
|
6.6
|
9
|
0.2
|
0.201
|
0.7
|
6
|
3.3
|
10
|
0.3
|
0.3
|
0.7
|
9.3
|
0
|
Figura 5. Gráfica de los datos de la tabla anterior para el experimento b2.
Figura 6. Gráfica del logaritmo natural de la absorbancia contra el tiempo para
determinar la constante de velocidad de reacción, k2. Obsérvese el
parecido de las pendientes.
Tabla 7. Datos de los coeficientes de regresión obtenidos para un orden de
reacción de uno para el experimento b2.
m
|
b
|
r
|
|
Tubo 6
|
-0.0058
|
0.1881
|
0.9981
|
Tubo 7
|
-0.0072
|
0.0592
|
0.9998
|
Tubo 8
|
-0.0087
|
0.0714
|
0.9997
|
Tubo 9
|
-0.011
|
0.3042
|
0.9999
|
Tubo 10
|
-0.013
|
0.2208
|
0.9997
|
Tabla 8. Datos para el cálculo de la dependencia de la constante de
pseudo-primer orden, k2, respecto a la fuerza iónica de las
soluciones.
Fuerza
iónica (M)
|
k2
|
ln
(I)
|
ln
k1
|
0.025
|
0.0058
|
-3.68887945
|
-5.14989736
|
0.05
|
0.0072
|
-2.99573227
|
-4.93367425
|
0.1
|
0.0087
|
-2.30258509
|
-4.74443225
|
0.2
|
0.011
|
-1.60943791
|
-4.50986001
|
0.3
|
0.013
|
-1.2039728
|
-4.34280592
|
Figura 7. Cálculo de la constante global de reacción, k’, para la relación k1=k’*In.
El valor de n obtenido fue de 0.319 y el valor de k’ de 0.0186259.
DISCUSIÓN
En la tabla 2 se muestran los resultados del experimento b1 en el
que se mantuvo constante la fuerza iónica mediante adición de NaCl 0.3 M y se
varió la concentración de NaOH. Éstos datos fueron utilizados para graficar la
Figura 1, donde se observa, como habría de esperar, que la absorbancia de la
muestra disminuye al pasar el tiempo. Se observa que para los tubos 1 y 2 las
curvas son aproximadamente lineales, que se comprueba con los coeficientes de
regresión de la Tabla 3 de 0.9928 y 0.982; sin embargo, para los tubos 3, 4 y 5
la tendencia no es lineal y los coeficientes de regresión son pobres, con
valores de 0.924, 0.883 y 0.8586, respectivamente. Por tanto la decoloración de
fenolftaleína no sigue una cinética de orden cero.
Para una cinética de orden uno se graficó el logaritmo natural de
la absorbancia contra el tiempo, como se puede apreciar en la Figura 2. La
tendencia es bastante lineal, comprobado con los datos de la Tabla 3 con
valores de coeficientes de regresión de 0.9979, 0.9987, 0.9969, 0.9968, y
0.9974 para los tubos 1-5, respectivamente, con un promedio de 0.9975. Por
tanto, se asume que sigue una cinética de pseudo-primer orden.
Aún así, se probó para una cinética de orden dos, en la que se
obtuvieron coeficientes de regresión buenos para los tubos 1 y 2 –como en el
caso de la cinética de orden cero- pero órdenes de regresión bajos para los
tubos 3-5.
Dado que la cinética es para un mismo reactivo y no depende de la
concentración de la especie que se desea medir sino de la naturaleza intrínseca
de los reactivos, productos, mecanismos de reacción y condiciones, se asume que
todos los tubos 1-5 y 6-10 deben seguir la misma cinética. En éste caso puesto
que todos se ajustaron bien a una de primer orden se asume que la reacción sí
sique una cinética de pseudo-primer orden.
Todo el procedimiento realizado anteriormente arrojó que para la
concentración de la especie reaccionante que absorbe a 550 nm (fenolftaleína)
el orden de reacción fue de 1. Sin embargo, se sabe que también el hidroxilo
participa en la reacción, por tanto también debe tener un orden de reacción que
estará determinado por la ecuación
. Sacando
logaritmos naturales obtenemos, lnk1= mlnCOH- + lnk.
Así que para determinar el orden de reacción de la concentración
de hidroxilo se procedió a graficar el logaritmo natural de las constantes
obtenidas, que equivalen a las pendientes negativas de la Tabla 3, contra el
logaritmo de la concentración de hidroxilo en cada uno de los tubos. La Figura 4 muestra que el coeficiente de
regresión para ésta recta es de 0.9980. Además los valores obtenidos para m
(pendiente) y k (eb) fueron de 1.0956 y 0.851036. Por tanto el orden
de reacción, m, es de uno. Así obtenemos
la ecuación general de velocidad de la reacción, que queda como
donde la concentración de fenolftaleína (F-2)
se mide en unidades de absorbancia y la concentración de OH- en
unidades de molaridad.
Una vez encontrada la ecuación general de degradación de
fenolftaleína, podemos proceder a determinar su validez. Para ello escogemos un
tubo al azar del experimento b1, en éste caso el tubo 4, y calculamos la
velocidad de degradación de la fenolftaleína haciendo uso de ésta fórmula.
Además se compara con el valor que se obtiene al dividir la diferencia de
absorbancias (ABS2-ABS1) entre la diferencia de tiempos
(t2-t1) que nos dará una aproximación del promedio de
velocidad en ese intervalo. Se puede apreciar en la siguiente figura que ambos
cálculos dan valores aproximadamente similares, siendo la línea naranja la más
exacta pues parte de diferenciación, mientras que los puntos azules sólo son
razones de cambio. Además se observa que conforme transcurre el tiempo, la
velocidad va disminuyendo, hecho que concuerda con lo esperado para una
reacción de pseudo-primer orden donde al disminuir la concentración de reactivo
(en éste caso fenolftaleína) va disminuyendo la velocidad de degradación.
Figura 8. Velocidad calculada para la cinética de
decoloración de fenolftaleína del tubo 4 usando dos técnicas: En azul se
muestra la técnica de velocidades diferenciales,
.
En naranja se muestra la velocidad calculada usando la fórmula ya obtenida de
velocidad,
,
donde la concentración de la especie F-2 está dada en unidades de
absorbancia y la de OH- es constante en toda la reacción e igual a
0.201 M. La fuerza iónica es constante e igual a 0.3 M.
La Tabla 6 muestra los resultados del experimento b2 donde se
mantuvo constante la concentración de NaOH (0.021 M) y se varió la fuerza
iónica de las soluciones de los tubos 6-10. La Figura 6 muestra el gráfico de
éstos dados de absorbancia contra tiempo. Se ve un comportamiento
aproximadamente lineal. No obstante, y como ya se determinó en el experimento
anterior, el orden de reacción es de pseudoprimer orden para la concentración
de fenolftaleína y no de orden cero. Así se tiene que graficar el logaritmo
natural de la absorbancia contra el tiempo. Se observa en la Figura 6 y Tabla 7
que el comportamiento sigue una cinética de primer orden, con un valor de
coeficiente de regresión promedio de
0.9994. Las pendientes nos ayudan a determinar el valor de k1 para
éstos tubos que se encuentran resumidos en la Tabla 8, donde además se resumen
las fuerzas iónicas de las soluciones de cada uno de los tubos.
Ahora la pregunta es, ¿afecta la fuerza iónica la velocidad de la
reacción?. Si la respuesta es no, se esperará que en los tubos 6-10 la
constante, k1, tenga un valor igual para cada uno de los tubos. Sin
embargo, como se ve en la siguiente figura la tendencia es que al aumentar la
fuerza iónica aumentará también la constante de reacción, es decir, a mayor
fuerza iónica la degradación de fenolftaleína ocurre más rápido.
Figura 9. Efecto de la fuerza iónica sobre la
constante cinética, k1, de decoloración de fenolftaleína. El valor
obtenido de la constante k1 para la concentración de 0.24 M de OH-
fue de 0.138 min-1.
El efecto de la fuerza iónica sobre la variación de la constante
de velocidad k1 se puede resumir en la siguiente ecuación:
donde I es la fuerza iónica de la solución.
Para determinar el valor de k y el valor de n se procede a sacar logaritmos,
así:
. Se obtiene
un valor de k de 0.0186259 y un valor de n de 0.319. Así la ecuación de la
cinética de degradación de fenolftaleína para la velocidad, queda como
que sólo aplica para una concentración de
hidroxilo de 0.021 M. Sin embargo, dado que la fuerza iónica (o NaCl) no es un
reactivo (o no se cree que lo sea) no se puede decir que el orden global de
reacción sea de 1.319. Simplemente es una relación empírica que relaciona el
efecto de la fuerza iónica sobre la velocidad de degradación de fenolftaleína.
Una vez encontrada ésta ecuación se procede a seleccionar un tubo
al azar, en éste caso el tubo 9 para comprobar la validez de la relación. Se
observa en la siguiente gráfica la velocidad medida sacando la variación de la
absorbancia respecto a la variación del tiempo en puntos azules, que dan una
aproximación de la velocidad promedio en cada intervalo, y en la línea naranja
se puede apreciar la aplicación de la ecuación obtenida donde la fuerza iónica
tiene un valor de 0.021 M para el tubo 9. Se puede apreciar que los puntos
azules presentan una leve tendencia descendente, o incluso tener en apariencia
valores constantes. Sin embargo, esto se debe a que el tiempo medido no fue
suficiente para ver una pendiente descendente más grande y apreciable. Esto lo
comprueba la línea naranja que tiene una pendiente sólo ligeramente negativa.
Figura 10. Velocidad de decoloración de la fenolftaleína en medio básico para el
tubo 9 donde la fuerza iónica tenía un valor de 0.201 M y la concentración de
OH- una concentración de 0.021 M. Los puntos azules muestran la
velocidad medida usando el método de diferenciales, donde
.
La línea naranja es la ecuación obtenida para el cálculo de la velocidad de
decoloración de fenolftaleína en la que se varía la fuerza iónica de la
solución,
La molecularidad de la reacción de degradación de fenolftaleína es
igual a dos que coincide con el orden de reacción global encontrado. La
reacción se puede resumir como:
Como se puede observar en la siguiente Figura el equilibrio de la
forma coloreada (2) a la forma incolora (3) se da por la adición de iones OH-2
presentes en el medio a valores de pH mayores a 10. Para el experimento el
valor mínimo de OH- presente fue de 0.021 M correspondiente a los
tubos 6-10. Ésta concentración tiene un pH de (14-log(0.021)) 12.3 que es mayor
a lo requerido para que se lleve a cabo la reacción.
Figura
11. Formas estructurales de la fenolftaleína
en disoluciones etanol-agua. 1) Forma incolora de fenolftaleína, presente a pH
menor a 8.0, se abrevia como H2F. 2) Forma coloreada de
fenolftaleína presente a pH 8.0-10, abreviada como F2-. 3) Forma
incolora, a pH mayor a 10, abreviada como FOH3.
La fuerza iónica es la concentración efectiva de iones presentes
en una solución. Afectó la velocidad de degradación de fenolftaleína porque según la teoría de
Debye-Hückey al
incrementarse la fuerza iónica por un aumento de la concentración o de la
valencia de los contraiones, se produce una disminución en la doble capa
eléctrica y un incremento en el gradiente de potencial (Atkins, 2008), lo que
se traduce en que la capa eléctrica de los iones OH- y F-2 será más
pequeña tal que los iones pueden interaccionar más íntimamente unos con otros
(pues al ser de la misma carga se repelen, pero al disminuir la capa eléctrica
la magnitud de la repulsión es menor). Además, incrementa el gradiente de
potencial necesario para que la reacción química ocurra. Es por ello que a
mayor fuerza iónica mayor es la velocidad de la degradación de color de
fenolftaleína.
CONCLUSIONES
·
Se logró
obtener una ecuación de pseudo-primer orden, con un r2 promedio de
0.9975, para la cinética de decoloración de fenolftaleína para la dependencia
velocidad de decoloración respecto a la concentración de la especie F-2.
·
Se logró
obtener una ecuación de segundo orden para la cinética de decoloración de
fenolftaleína que depende de la concentración de F-2 y de OH-,
ambos con coeficientes parciales de primer orden.
·
La ecuación
obtenida para la cinética de decoloración de fenolftaleína en medio básico es
·
Aumentar la
concentración de fenolftaleína o de oxhidrilos aumenta la velocidad de
decoloración de fenolftaleína en medio básico.
·
Aumentar la
fuerza iónica de la solución aumenta la velocidad de decoloración de
fenolftaleína pero no en el mismo grado que aumentarla con la adición de OH-.
BIBLIOGRAFÍA
·
Atkins, P.
(2008). Química física (8a ed.).
Madrid: Editorial Médica Panamericana
·
Barrante, J. R. (1998). Applied Mathematics for Physical Chemistry (2ª
ed.). Nueva Jersey: Prentice Hall, pp.
56-58
·
Castellan,
G. (1987). Fisicoquímica (2a ed).
México: Addison Wesley Iberoamericana
·
Rogers, D. (2011). Consice Physical Chemistry (1ª ed.). Nueva Jersey: John Wiley & Sons
·
Wittaker, A.G., Mount, A.R. y Heal, M.R. (2000). Instant notes in Physical Chemistry (1ª ed.). Nueva York: Springer Verlag, pp. 615-625.
ANEXOS
Memoria de cálculos
Integración de velocidades para orden cero, uno y dos
Para el caso
del orden cero tenemos:
Por tanto:
Entonces
podemos integrar sin límites y obtener:
Así que al
graficar la concentración de fenolftaleína (o absorbancia) contra el tiempo
obtenemos la pendiente que es igual a –k.
Para el
caso de orden uno;
Al integrar
sin límites tenemos,
Así que al
graficar el logaritmo natural de la concentración o absorbancia contra el tiempo tenemos una
pendiente que es igual a el negativo de la constante.
Para orden dos:
Así que al
graficar el inverso de la concentración o absorbancia contra el tiempo tenemos
una pendiente que es igual a la constante de velocidad.
Tablas
Tabla 9. Datos del tubo 4 para la Figura 8.
Tiempo
(min)
|
Absorbancia
|
Velocidad
medida
|
Velocidad
calculada
|
0
|
0.909
|
0.15549194
|
|
0.5
|
0.833
|
0.152
|
0.14249151
|
1
|
0.766
|
0.134
|
0.13103061
|
1.5
|
0.703
|
0.126
|
0.12025394
|
2
|
0.647
|
0.112
|
0.11067468
|
2.5
|
0.595
|
0.104
|
0.10177965
|
3
|
0.548
|
0.094
|
0.09373991
|
3.5
|
0.505
|
0.086
|
0.08638441
|
4
|
0.466
|
0.078
|
0.07971314
|
4.5
|
0.43
|
0.072
|
0.07355504
|
5
|
0.397
|
0.066
|
0.06791012
|
5.5
|
0.367
|
0.06
|
0.06277837
|
6
|
0.339
|
0.056
|
0.05798874
|
6.5
|
0.314
|
0.05
|
0.05371229
|
7
|
0.291
|
0.046
|
0.04977795
|
7.5
|
0.27
|
0.042
|
0.04618572
|
8
|
0.25
|
0.04
|
0.04276456
|
8.5
|
0.232
|
0.036
|
0.03968551
|
9
|
0.216
|
0.032
|
0.03694858
|
9.5
|
0.201
|
0.03
|
0.03438271
|
10
|
0.187
|
0.028
|
0.03198789
|
10.5
|
0.174
|
0.026
|
0.02976413
|
11
|
0.163
|
0.022
|
0.02788249
|
11.5
|
0.152
|
0.022
|
0.02600085
|
12
|
0.142
|
0.02
|
0.02429027
|
12.5
|
0.133
|
0.018
|
0.02275075
|
13
|
0.125
|
0.016
|
0.02138228
|
13.5
|
0.118
|
0.014
|
0.02018487
|
14
|
0.111
|
0.014
|
0.01898746
|
14.5
|
0.105
|
0.012
|
0.01796111
|
15
|
0.099
|
0.012
|
0.01693477
|
15.5
|
0.093
|
0.012
|
0.01590842
|
16
|
0.088
|
0.01
|
0.01505312
|
Tabla 10. Datos del tubo 9 para la Figura 10.
Tiempo
(min)
|
Absorbancia
|
Velocidad
medida
|
Velocidad
calculada
|
0
|
1.356
|
0.01513898
|
|
0.5
|
1.348
|
0.016
|
0.01504966
|
1
|
1.341
|
0.014
|
0.01497151
|
1.5
|
1.333
|
0.016
|
0.01488219
|
2
|
1.326
|
0.014
|
0.01480404
|
2.5
|
1.318
|
0.016
|
0.01471473
|
3
|
1.311
|
0.014
|
0.01463658
|
3.5
|
1.305
|
0.012
|
0.01456959
|
4
|
1.297
|
0.016
|
0.01448027
|
4.5
|
1.29
|
0.014
|
0.01440212
|
5
|
1.283
|
0.014
|
0.01432397
|
5.5
|
1.276
|
0.014
|
0.01424582
|
6
|
1.27
|
0.012
|
0.01417883
|
6.5
|
1.262
|
0.016
|
0.01408952
|
7
|
1.255
|
0.014
|
0.01401137
|
7.5
|
1.248
|
0.014
|
0.01393322
|
8
|
1.241
|
0.014
|
0.01385507
|
8.5
|
1.235
|
0.012
|
0.01378808
|
9
|
1.228
|
0.014
|
0.01370993
|
9.5
|
1.221
|
0.014
|
0.01363178
|
10
|
1.214
|
0.014
|
0.01355363
|


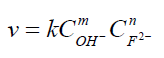
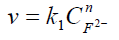
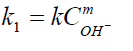























como calculan los datos de la tabla 1
ResponderEliminarNo lo sè
Eliminar??
ResponderEliminary las formulas de la I???
ResponderEliminar